NumPy

NumPy入門 メッシュグリッドと可視化

このページではデータを可視化する際によく使用するメッシュグリッドと呼ばれる配列生成関数について学習します。

meshgridとは

配列X=[1, 2, 3]、Y=[-1, 0, 1]が与えられていたとします。これらの格子点、つまりXとYの組み合わせは(1, 0)、(2, 0)、(3, 0)、(1, 1)、(2, 1)、(3, 1)、(1, -1)、(2, -1)、(3, -1)の9つとなりますが、meshgridを使用するとそれらをプログラム上で扱いやすい形で出力されたX, Yの組を得ることができます。

サンプルで具体的に確認してみましょう。

X = [1, 2, 3]
Y = [-1, 0, 1]
xv, yv = np.meshgrid(X, Y)
xv
# array([[1, 2, 3],
#        [1, 2, 3],
#        [1, 2, 3]])
# 

yv
# array([[-1, -1, -1],
#        [ 0,  0,  0],
#        [ 1,  1,  1]])
#

少しわかりづらい構造ですが、以下のように2回ループで順番に要素を取り出すと前述の直積、9つの要素が得られることが確認できます。

for xx, yy in zip(xv, yv):
    for x, y in zip(xx, yy):
        print(x, y)
# 1 -1
# 2 -1
# 3 -1
# 1 0
# 2 0
# 3 0
# 1 1
# 2 1
# 3 1
#

meshgridを利用した可視化

とっつきづらい構造ですが、ユニバーサル関数と相性がよく、グリッド上の関数の評価する際に非常に便利です。（公式より「meshgrid is very useful to evaluate functions on a grid.」）

また、評価結果をそのままmatplotlibに指定して出力することが可能です。

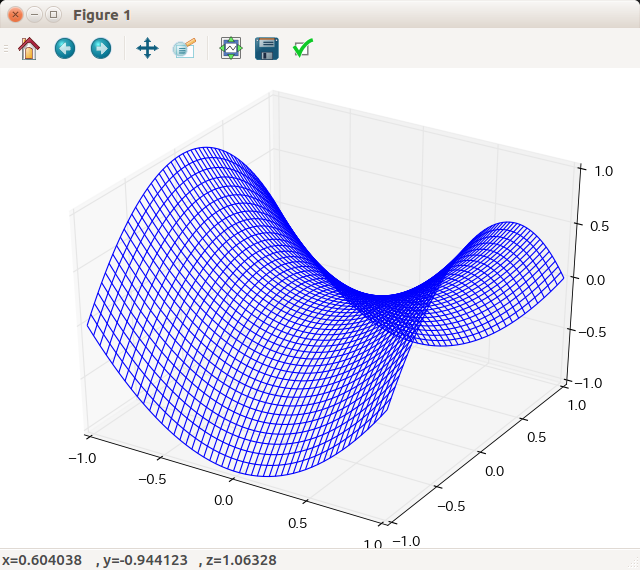
サンプルです。教養課程の微積の鞍点の説明でよく使用される関数\( z = x^2 - y^2 \)について、定義域\( [-1, 1] \times [-1, 1] \)の様子を可視化して確認してみましょう。ユニバーサル関数np.subtractにそのまま値を指定することができている点に注目してください。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 定義域[-1, 1]のx, yを50個区切りで生成
x = np.linspace(-1, 1, 50)
y = np.linspace(-1, 1, 50)

# メッシュグリッドを生成
xv, yv = np.meshgrid(x, y)


# 関数x^2 - y^2の値をzに代入
z = np.subtract(xv**2, yv**2)

# x, y, zをワイヤフレームで表示
ax = Axes3D(plt.figure())
ax.plot_wireframe(xv, yv, z)
plt.show()

以下のようにグラフが出力され、各点におけるzの値（＝高さ）を確認することができます。