NumPyの乱数の練習として、モンテカルロ法のサンプルを掲載します。(一様分布の乱数であれば何でも良いため、NumPyではなく組み込みのrandomモジュールを使用しても問題はありません。)
Contents
円周率を求める
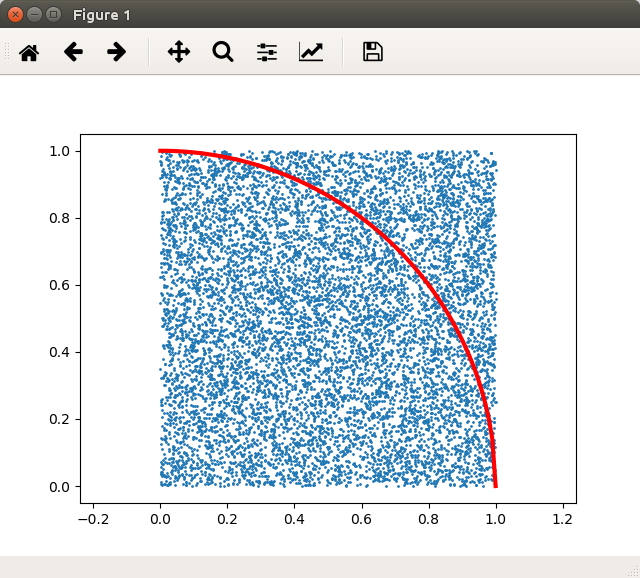
2次元平面上に\( [0, 1] \times [0, 1] \)の一様分布のランダムな点を生成し、円の内側の点の比率を算出します。理論上、この比率が円周率の1/4となるはずです。
import numpy as np
from matplotlib import pyplot as plt
def is_inner(x, y):
"""
円の内側かどうかを判定
"""
return x ** 2 + y ** 2 < 1
inner_points_cnt = 0
all_points_cnt = 0
X, Y = np.random.rand(2, 10 ** 4)
for x, y in zip(X, Y):
all_points_cnt += 1
if is_inner(x, y):
inner_points_cnt += 1
pi = (inner_points_cnt / all_points_cnt) * 4
# 計算結果を表示
print(pi)
# 以下matplotlibによる可視化
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
# ランダムに配置した点
ax.scatter(X, Y, s=1)
# x ** 2 + y ** 2 = 1 のグラフ
cx = np.linspace(0, 1, 100)
cy = np.sqrt(np.subtract(1, cx ** 2))
ax.plot(cx, cy, linewidth=3, color='r')
# 縦横比をそろえる
plt.gca().set_aspect('equal', adjustable='box')
# グラフの表示
plt.show()
点は\( 10^4 \)個生成し、私の環境では小数点第1位までは正確に算出することができました。生成する点の数を増やすとさらに精度を上げることができます。
三角関数の面積を求める
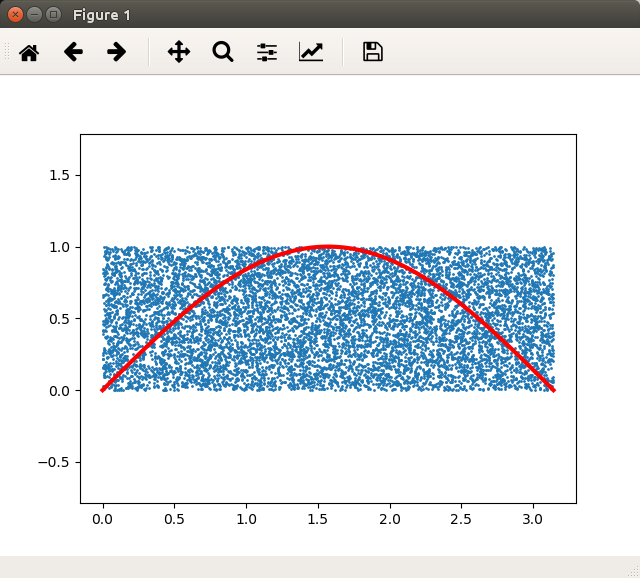
もう1つサンプルです。2次元平面上に\( [0, \pi] \times [0, 1] \)の一様分布の乱数を生成し、\( sin(x) \)の内側の点の比率を求めることにより、\( \int _0 ^\pi sin(x) dx \)の値を求めてみます。
import numpy as np
from matplotlib import pyplot as plt
def is_inner(x, y):
"""
sin(x)の内側かどうかを判定
"""
return y < np.sin(x)
points_num = 10 ** 4 # 生成する点の数
inner_points_cnt = 0 # 内側の点のカウンタ
X = np.random.rand(points_num) * np.pi
Y = np.random.rand(points_num)
for x, y in zip(X, Y):
if is_inner(x, y):
inner_points_cnt += 1
S = (1 * np.pi) * (inner_points_cnt / points_num)
# 計算結果を表示
print(S)
# 以下matplotlibによる可視化
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
# ランダムに配置した点のプロット
ax.scatter(X, Y, s=1)
# y = sin(x) のグラフ
cx = np.linspace(0, np.pi, 100)
cy = np.sin(cx)
ax.plot(cx, cy, linewidth=3, color='r')
# 縦横比をそろえる
plt.gca().set_aspect('equal', adjustable='box')
# グラフの表示
plt.show()
実際に手で計算してみると\( \int _0 ^\pi sin(x) dx = 2\)となります。私の環境だと1.98でしたので、そこそこの精度で解が得られたことになります。
複雑な積分計算も近似値が単純な計算で得られる点が大きなメリットです。
上の両サンプルでは、ランダムな点を先に生成しているためメモリの使い方としてはイマイチですね。生成する乱数の数が膨大になると少々不安があります。精度を上げるため生成する乱数を増やす場合はwhile文にしてループ内で都度乱数を生成するなどして工夫してみてください。




