今回はシミュレーションやテストデータを作成する際によく使う乱数についてです。
randomモジュールとrand
NumPyのrandomモジュールには様々な乱数を生成するメソッドが用意されています。まずは基本的なrandメソッドについて学習しましょう。
rand
randメソッドを使用すると、最も基本的な乱数である[0, 1)区間(0.0以上、1.0未満)の一様乱数を生成することができます。
引数で生成する要素数を指定します。
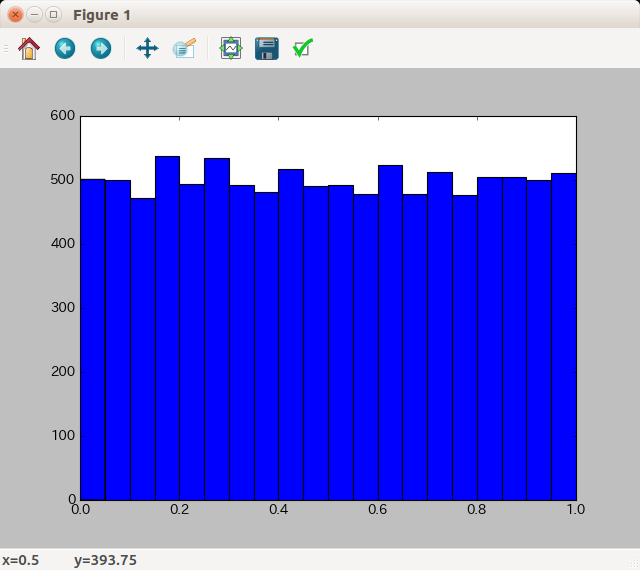
10000個の乱数を生成し、階級数が20のヒストグラムで可視化するサンプルを見てみましょう。
import numpy as np import matplotlib.pyplot as plt rand_array = np.random.rand(10000) fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.hist(rand_array, bins=20, ec="b") plt.show()
多次元の乱数
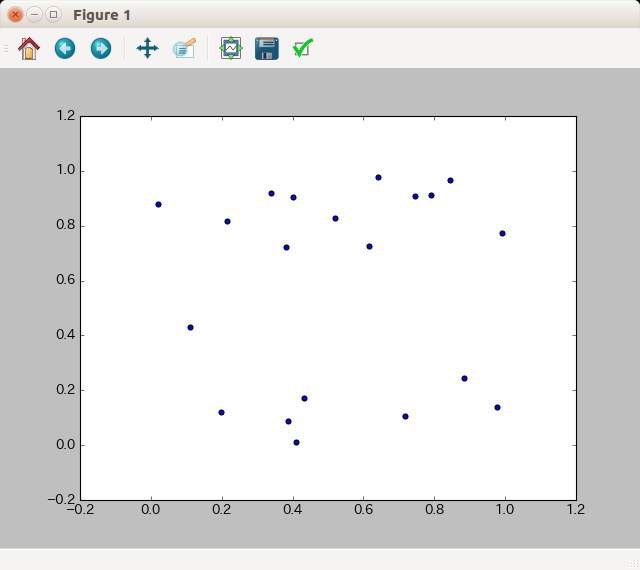
第二引数以降を指定すると、その次元の乱数行列が返されます。2x20の行列を生成してプロットしてみましょう。
import numpy as np import matplotlib.pyplot as plt rand_x, rand_y = np.random.rand(2, 20) fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.scatter(rand_x, rand_y) plt.show()
さまざまな分布の乱数
さまざまな分布の乱数
randomモジュールには様々な分布の乱数を生成するメソッドが用意されています。代表的なものを紹介します。
| メソッド | 分布 |
|---|---|
| beta | ベータ分布 |
| binomial | 二項分布 |
| chisquare | カイ二乗分布 |
| dirichlet | ディリクレ分布 |
| exponential | 指数分布 |
| f | F分布 |
| gamma | ガンマ分布 |
| geometric | 幾何分布 |
| gumbel | ガンベル分布 |
| hypergeometric | 超幾何分布 |
| logistic | ロジスティック分布 |
| lognormal | 対数正規分布 |
| logseries | 対数級数分布 |
| multinomial | 多項分布 |
| multivariate_normal | 多変量正規分布 |
| negative_binomial | 負の二項分布 |
| noncentral_chisquare | 非中心カイ二乗分布 |
| noncentral_f | 非中心F分布から |
| normal | 正規分布 |
| poisson | ポアソン分布 |
| standard_cauchy | 標準コーシー分布 |
| standard_exponential | 標準指数分布 |
| standard_gamma | 標準ガンマ分布 |
| standard_normal | 標準正規分布 |
| standard_t | 標準t分布 |
| uniform | 一様分布 |
| weibull | ワイブル分布 |
その他の分布の乱数や、引数については以下を参照してください。
Random sampling
サンプル
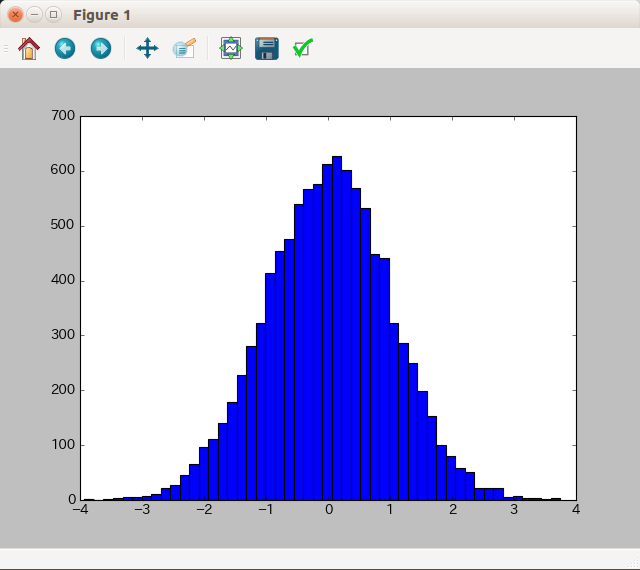
例として標準正規分布をヒストグラムで可視化してみましょう。
import numpy as np import matplotlib.pyplot as plt rand_array = np.random.standard_normal(10000) fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.hist(rand_array, bins=50, ec="b") plt.show()
randと異なり、釣鐘状の分布となっていることが確認できます。