NumPy入門 行列の計算 回転行列の計算例

肩慣らしとして今回は具体的かつ簡単な行列の計算例として回転行列による一次変換を取り上げてみます。

回転行列による一次変換

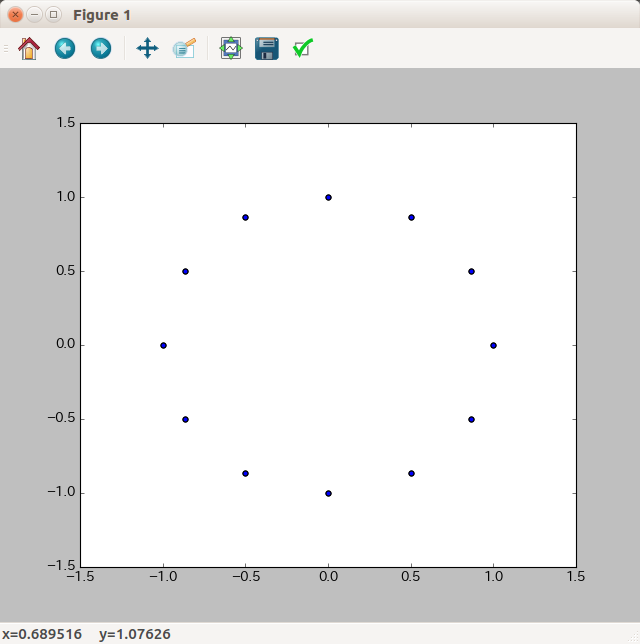
平面座標上の始点(0, 1)に対し、回転行列により30度ずつ回転移動させてみます。移動させた点をmatplotlibで可視化してみます。

NumPyでは三角関数のsin、cosがnp.sin、np.cosとして提供されていますので回転行列の各要素でそれらを使用します。

行列の掛け算では前回学習したnp.dotを使用します。

import matplotlib.pyplot as plt
import numpy as np


def get_rotation_matrix(rad):
    """
    指定したradの回転行列を返す
    """
    rot = np.array([[np.cos(rad), -np.sin(rad)],
                    [np.sin(rad), np.cos(rad)]])
    return rot


# 始点
base_point = np.array([1, 0])
x_points = []
y_points = []

for i in range(0, 12):
    deg = i * 30
    rad = deg * np.pi / 180
    rot = get_rotation_matrix(rad)
    rotated = np.dot(rot, base_point)
    x_points.append(rotated[0])
    y_points.append(rotated[1])

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.scatter(x_points, y_points)
ax.grid(True)

plt.gca().set_aspect('equal', adjustable='box')
plt.show()

上のスクリプトを実行すると、以下のようにグラフが描画され、一次変換によって回転移動されていることを確認することができます。