これまで、データの特徴をとらえるため平均や分散などの統計量について学習してきました。ここからは少し難しくなりますが、確率変数について学習しましょう。
Contents
確率変数と分布
離散型確率変数
サイコロの目のように各変数に対して確率が与えられている場合、それらの各変数を確率変数と呼びます。確率的に色々な値を取りうる変数ともいえます。確率変数がとる分布を確率分布と呼びます。
また、6面のサイコロは√2などの間は存在せず、飛び飛びの値をとりますが、このような確率変数を離散型確率変数と呼びます。一方、連続的な値を取る確率変数もあり連続型確率変数と呼びますが、まずは離散型確率変数から解説します。
6面のサイコロを適当に振ると1〜6の目はそれぞれ1/6の確率で出現します。また、それ以外の目が出る確率はありえないので0となります。
| 確率変数 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 確率 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
サイコロの出る目の確率の関数をとして表すと以下のようになります。このような離散型確率変数の関数を確率質量関数と呼びます。英語ではprobability mass functionと呼ばれ、PMFと略されることがあります。
\[f(X) = \begin{cases}
1/6 & (xが1, 2, 3, 4, 5, 6 のいずれか) \\
0 & (上記以外)
\end{cases} \]
グラフにすると以下のようになります。X軸が確率変数、グラフの高さが確率です。
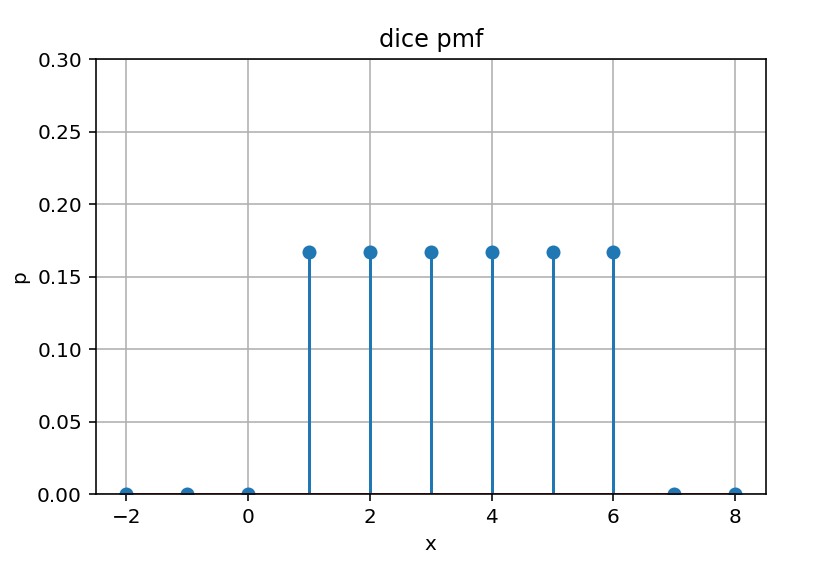
グラフを見ると、1〜6の各値で確率1/6が、それ以外の点は確率0となっていることが表されているということがわかります。上のグラフのとおり、離散型確率変数はXのある点に対してYの確率が定義されます。
連続型確率変数
サイコロやクジなど、離散型の確率は中学・高校の数学の授業で扱うため比較的馴染みがありますが、統計を学ぶ上でもう一つ重要なのが連続型確率変数です。
まず、クイズからやってみましょう。
クイズ
以下のような回転するボードに吹き矢を当ててみる。ボードには角度が振られている。吹き矢はボードのどこかにランダムに命中するものとする。また、ボードから外れることはないものとする。
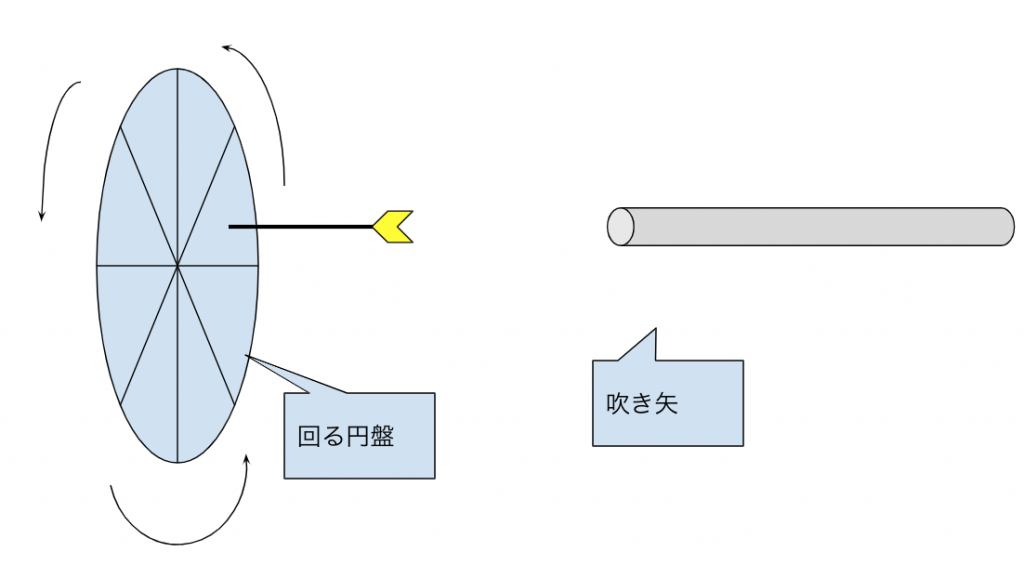
(1) 0度〜90度の間に命中する確率を求めよ
(2) 90度の線にきっちり命中する確率を求めよ
さて、わかったでしょうか?
まず、(1)の答えは1/4となります。どの点でもランダムに当たるので、全体の1/4領域である0度〜90度の場所に命中する確率は1/4となります。
(2)なのですが、答えは0となります。こちらは悩まれた方が結構いるのではないでしょうか。角度のように連続な値をとるものは、任意の一点が発生する確率は0となります。雑な説明をすると、点の数は∞なので、ある点に命中する確率は1/∞=0となります。
角度のような連続的な値をとる確率変数を連続型確率変数と呼びます。上の円盤の角度\(-\pi\sim\pi\)(単位はラジアンとします。)を確率変数としてみなしたときの関数は以下のようになります。
\[f(X) = \begin{cases}
1/(2\pi) & (-\pi <= x < \pi) \\
0 & (上以外の場合)
\end{cases} \]
このような連続型確率変数の確率の関数を確率密度関数と呼びます。英語だとprobability density functionで略してPDFと呼ばれることがあります。先程の関数をグラフで表すと以下のようになります。
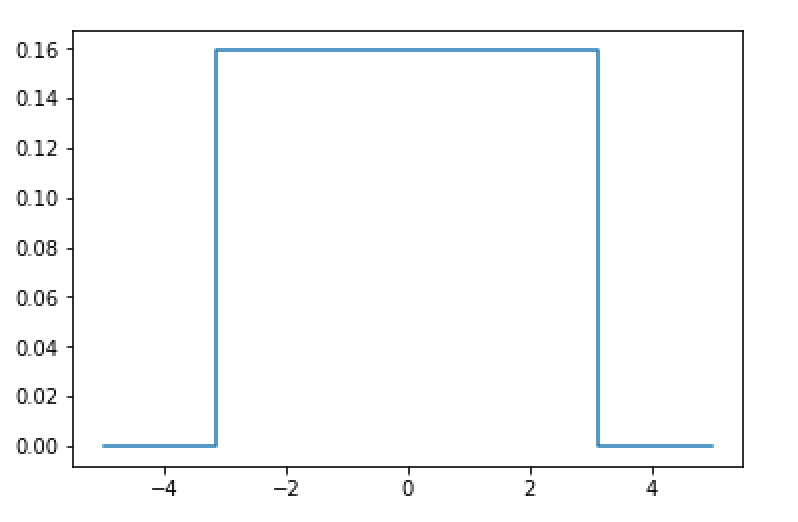
グラフの見方なのですが、指定範囲での確率密度関数とx軸囲まれた部分の面積がその範囲が起こりうる確率となります。
例えば、先程の0度〜90度\(0\sim\frac{\pi}{2}\)の間に命中する確率の場合の確率を図示した場合、以下のようになり、囲まれた部分の面積は1/4です。この1/4が吹き矢が0度〜90度の間に命中する確率となります。
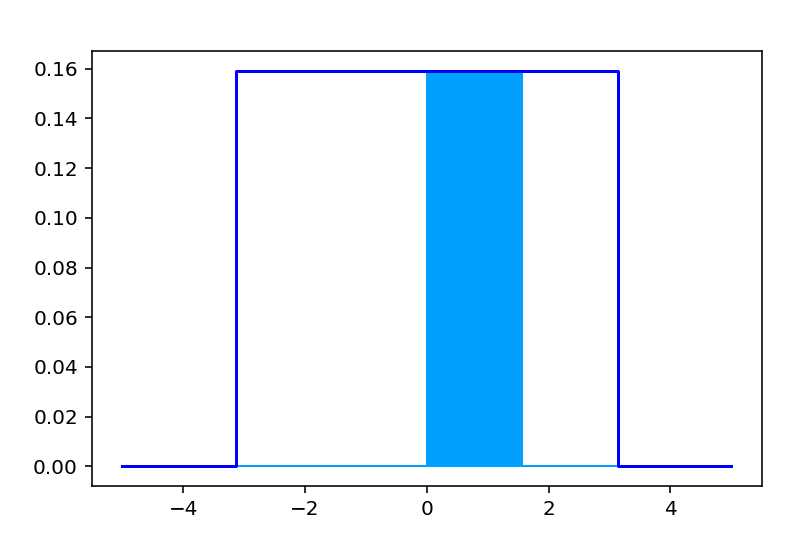
また、確率密度関数とx軸で囲まれた部分の面積は1となりますが、これは全事象の確率を表します。一方で任意の点の発生する確率は0となります。1つの点に対応する高さにはあまり意味がなく、重要なのは連続型確率変数は点ではなく範囲で扱う、ということです。
この円盤の角度の例のような特定の範囲が一定の分布を一様分布と呼びます。少々難しい内容でしたがここを押さえれば今後、特定の分布であればPythonで自由に範囲の確率を求めることができるようになります。
次回、連続型確率分布で最も重要と言われている正規分布について解説します。