正規分布

前回、離散型と連続型の確率変数と確率分布について学習しました。今回は連続型確率分布で最も重要と言われている正規分布について解説します。

正規分布とは

ある確率変数Xが以下の確率密度関数で表される分布を正規分布と呼びます。expは指数関数を表します。
\[
f(X) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp{[-\frac{(x-\mu)^2}{2\sigma^2}]}
\]

非常に複雑ですね。この講座では覚える必要はありませんが、名前と特徴はしっかりと知っておく必要があります。正規分布のグラフは以下のような形となります。

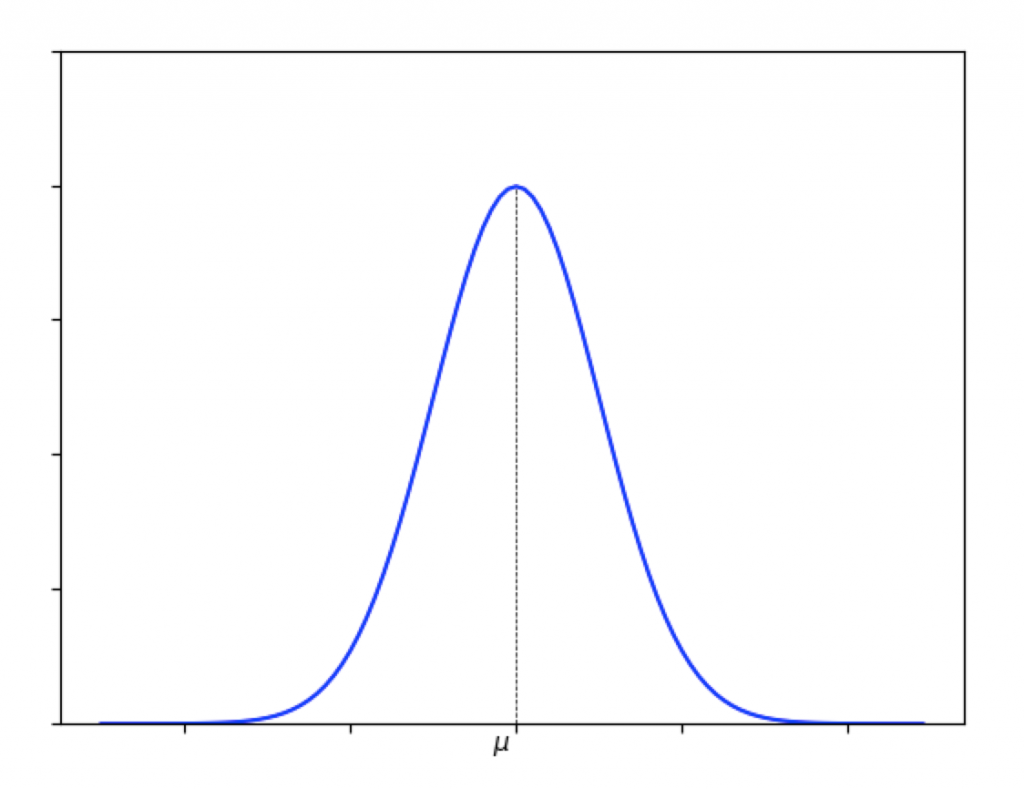
まず目につく特徴として平均μを中心とした左右対称の釣鐘型の分布となります。鐘の形に似ていることからベル・カーブ（鐘形曲線）とも呼ばれることもあります。自然界ではこの分布をとるものが多く見られます。

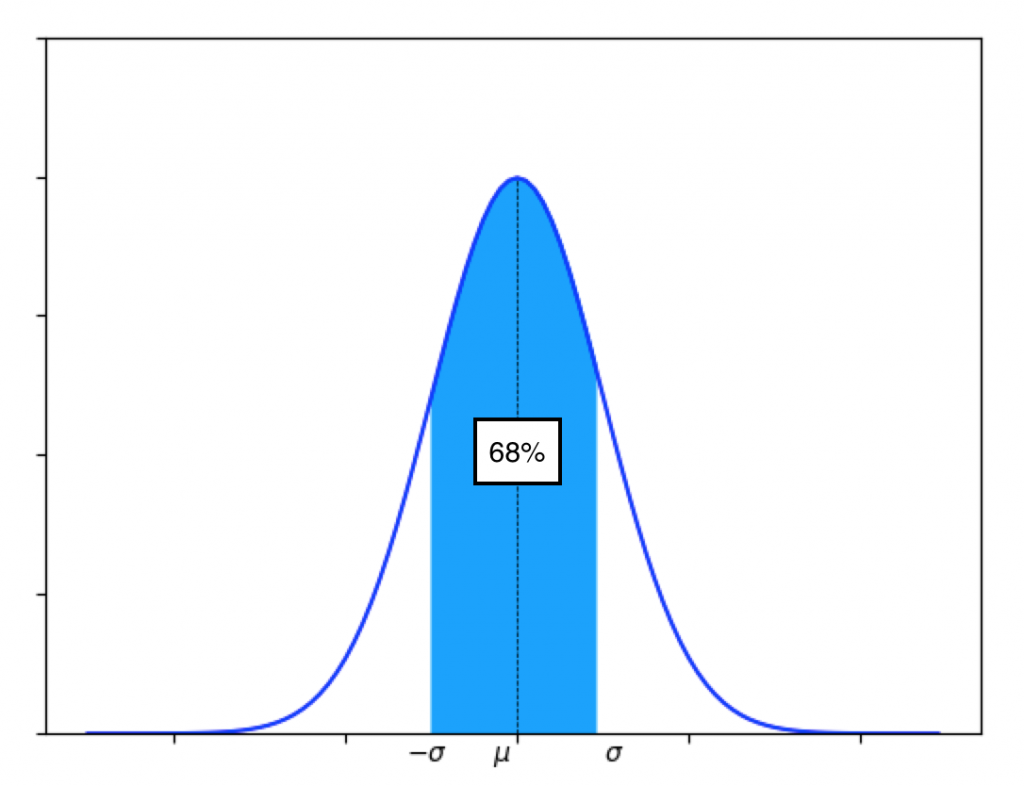
また、平均±σの範囲にデータの68%が、平均±2σの範囲にデータの95%が含まれます。

平均±σ

平均±2σ

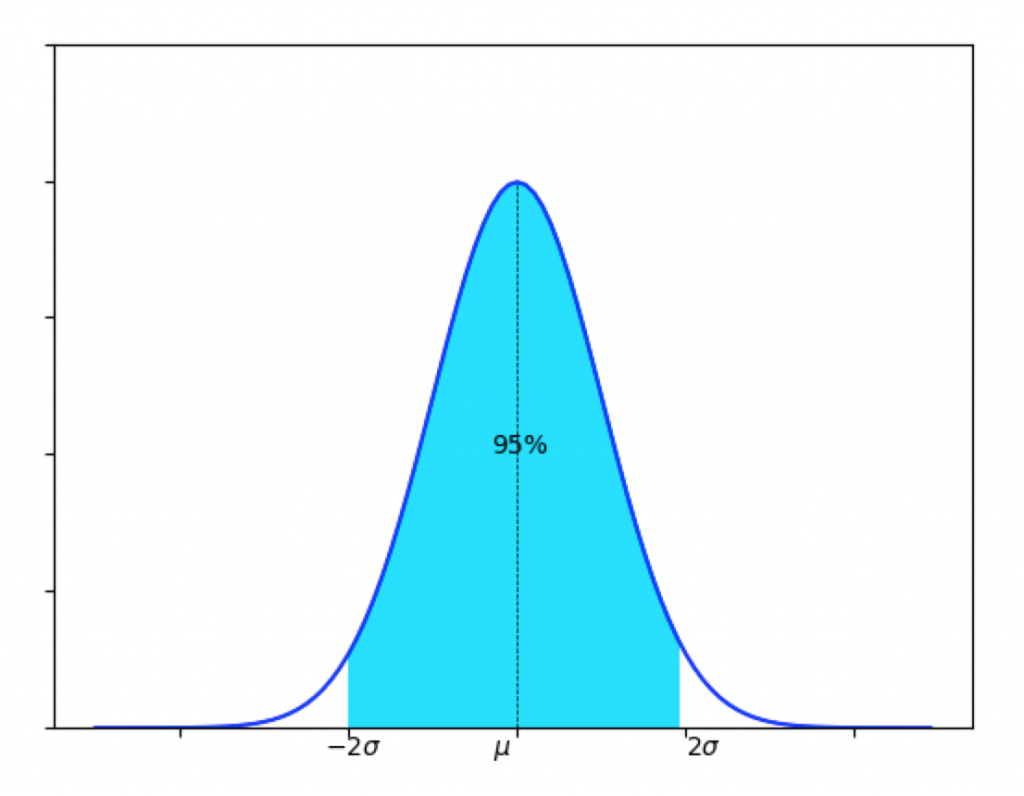
少々乱暴ですが、正規分布であれば平均±2σの範囲に殆どのデータが収まると言えるわけですね。

せっかくなので特徴を掴むために手を動かしてみましょう。以下のPythonコードで正規分布のグラフを描画することが可能です。平均と標準偏差を色々変えてグラフを観察してみてください。

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

# 平均
loc = 10
# 標準偏差
scale = 10

# 左端（平均-5*σ）
start = loc - scale * 5

# 右端（平均+5*σ）
end = loc + scale * 5

# X軸
X = np.arange(start, end, 0.1)
# 正規分布pdf生成
Y = norm.pdf(X, loc=loc, scale=scale)

# プロットする
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.grid(color='gray')
ax.plot(X, Y, color='blue')
plt.show()

なお、次回以降解説する予定ですが、norm.pdfで正規分布の確率密度関数を得ることが可能です。以下の書式となります。

パラメトリックな分布

正規分布は統計学的に良い性質を色々持っているのですが、その１つがパラメトリックな分布である、という点です。難しい単語ですが簡単に書くと「いくつかのパラメータ（統計量のこと）さえわかれば全体の様子がわかる」という分布です。

正規分布の場合は平均と分散or標準偏差という２つのパラメータさえわかってしまえば分布全体のことを把握することができます。

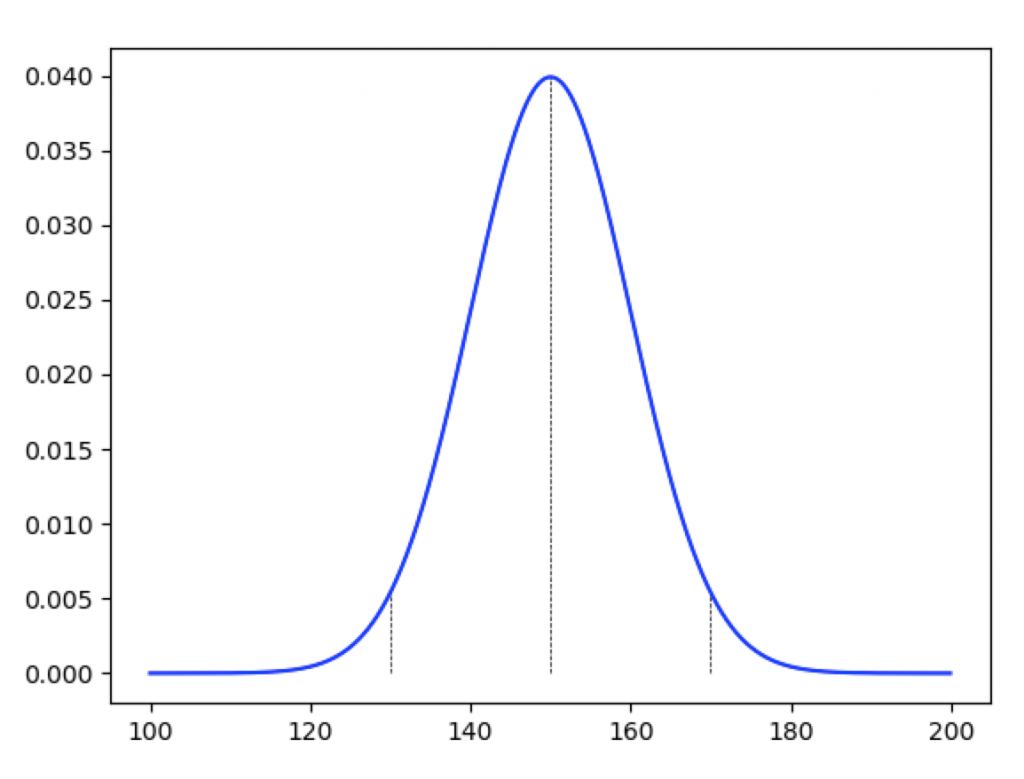
例えば、ある農園の人参の重量が平均が150g、分散が10^2の正規分布に従うとします。この場合、先程の正規分布の性質を利用すると、この農園の人参の重量は95%が130g〜170g（μ±σ^2=150±20g）の間に収まるといえます。また、170gの人参があった場合、おおよそ上位2.5%以内に入ると推定することができるのです。

ある農園の人参の重量分布

用語の補足

分布には正規分布以外に様々な種類がありますが、確率変数がある確率分布をとるとき、「従う」と呼びます。例えば、「この花の花弁の長さは正規分布に従う」「この製品の寿命は指数分布に従う」などといった使い方をします。

多くのパラメトリックな分布には対応する記号が与えられています。例えば、平均\(\mu\)、分散\(\sigma^2\)となる正規分布の場合、\(N(\mu,\sigma^2)\)と表します。さらに、確率変数\(X\)が正規分布\(N(\mu,\sigma^2)\)に従うとき以下ので表します。

\[
X \sim N(\mu,\sigma^2)
\]

標準化と標準正規分布

正規分布の場合、標準化という操作を行うことがあります。平均や分散が異なる正規分布の集合を比較する際によく使用します。標準化とは下式の通り、ある確率変数Xに対し平均\(\mu\)からの距離を標準偏差で割り算する変換を指します。
\[
Z = \frac{X-\mu}{\sigma}
\]

確率変数\(X\)が正規分布\(N(\mu,\sigma^2)\)に従うとき先程の変換した変数\(Z\)は正規分布\(N(0,1)\)に従います。
\[
f(X) = \frac{1}{\sqrt{2\pi}}exp{[-\frac{x^2}{2}]}
\]

この平均0、分散1の正規分布を標準正規分布と呼びます。正規分布を一旦標準正規分布に変換して計算しやすくする、という操作は統計計算で頻繁に使うのですが、Pythonを使用するとPythonがそういった計算を肩代わりしてくれるので筆算時と比較すると使う機会が比較的少ないといえそうです。