前回、区間推定の例として母分散が既知の場合の母平均の区間推定について解説しました。おそらく多くの方が、母平均が知りたいのに母分散が既知の場合なんてあるのだろうか?と思われたのではないでしょうか?お察しの通り、そもそも母分散が予めわかっている場合というのはあまりありません。実際によく使われるのがt分布を利用した区間推定です。このページでは母分散が不明な場合に母平均を区間推定する方法について解説します。
Contents
t分布
まずは公式から紹介します。母分散が正規分布の場合に標本サイズNの標本を採取したとします。この時、標本に関する以下の値は自由度N-1のt分布という分布に従います。
\[
t = \frac{\overline{X} - \mu}{\sqrt{S^2/N}}
\]
前回と異なり、母分散の\(\sigma^2\)ではなく標本不偏分散の\(S^2\)となっている点に注意してください。
ではt分布について解説します。t分布は0を中心とした左右対称の釣鐘型の分布で、標本数Nに関連する自由度という添え数を持ちます。以下のグラフは自由度1、4、20のt分布のグラフです。自由度が上がるにつれ尖ってきます。
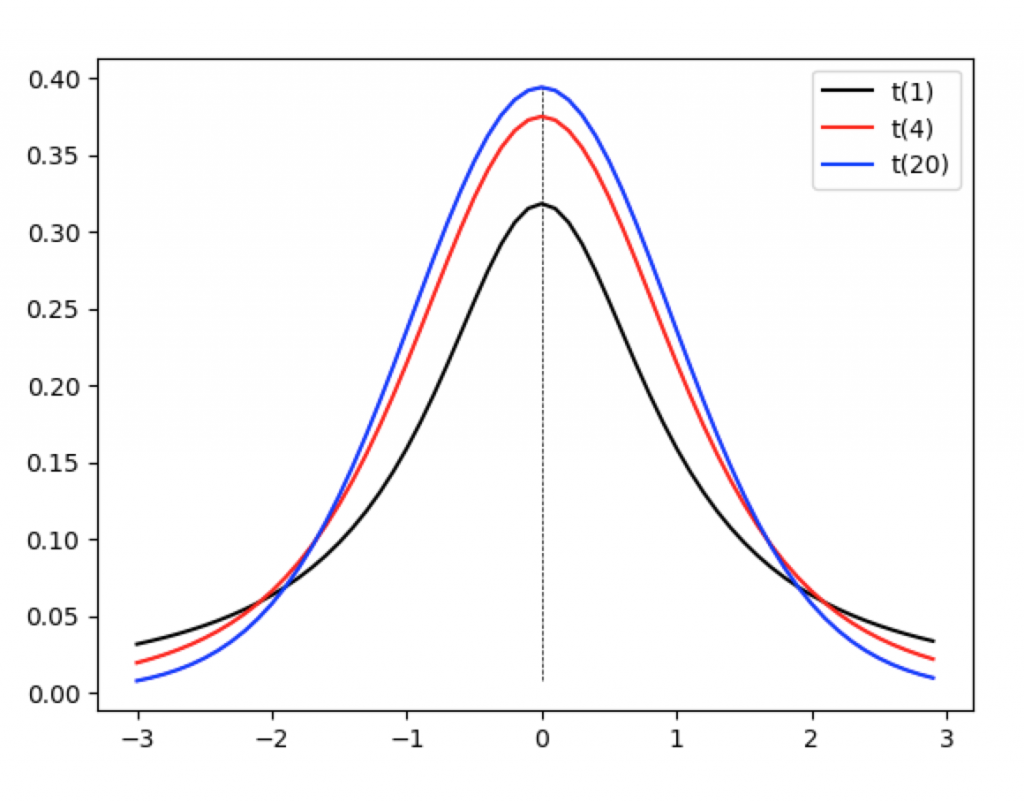
上のプロットは以下のコードで描画しています。
import numpy as np from scipy.stats import t import matplotlib.pyplot as plt # figure、ax生成 fig = plt.figure() ax = fig.add_subplot(1, 1, 1) # X軸 X = np.arange(-3, 3, 0.1) Y = t(1).pdf(X) ax.plot(X, Y, color='#000000', label="t(1)") Y = t(4).pdf(X) ax.plot(X, Y, color='red', label="t(4)") Y = t(20).pdf(X) ax.plot(X, Y, color='blue', label="t(20)") ax.legend() ax.vlines(0, min(Y), max(Y), linestyle='dashed', linewidth=0.5) plt.show()
正規分布に似ていますが、実際自由度が増えるについて正規分布に近似できることが知られており、自由度が30を超える場合は正規分布を利用する場合があります。
途中式は割愛しますが、上の公式から以下のように母平均\(\mu\)について信頼係数\(\alpha\)の信頼区間の公式を導出することができます。
\[
\overline{X} - t_{N-1}(\alpha/2) \sqrt{S^2/N} < \mu < \overline{X} + t_{N-1}(\alpha/2)\sqrt{S^2/N}
\]
なお、\(t_{N-1}(\alpha/2)\)は自由度N-1のt分布の\({\alpha/2} \times 100\)%点を表します。母平均\(\mu\)が\(\alpha\times 100\)%の確率で上の不等式の範囲に収まるということになります。
t分布のパーセント点
次に、Pythonでt分布を利用するためにパーセント点の求め方を解説します。scipy.statのtを使用します。正規分布と同様、パーセント点を求める場合はppfを使用します。引数に確率と自由度を指定します。例えば自由度19のt分布の上側2.5%点を求める場合は以下のように記述します。
from scipy.stats import t p_975 = t.ppf(0.975, 19) # 2.093024054408263
具体的な計算例
それでは実際にt分布を利用して区間推定をしてみましょう。前回、前年の分散を使用するという少々無理のある設定でしたが今回は標本データのみから母平均を区間推定します。
例
ある農園でみかん20個の重量を計測すると、以下のリストの通りとなった。この農園のみかんの重量は正規分布していることがわかっている。農園全体のみかんの平均重量について95%の信頼区間を求めてみる。
# 標本データ samples = [128.4, 135.9, 126.5, 182.4, 157.6, 100.6, 176.4, 126.6, 146.1, 138.0, 167.7, 128.1, 156.1, 183.5, 133.2, 162.4, 169.0, 161.6, 127.7, 154.3]
標本不偏分散を求め、前回同様に標本サイズと分布の上側2.5%点を求めて公式に当てはめます。
import numpy as np from scipy import stats # 標本分散 S2 = np.var(samples, ddof=1) # 標本サイズ N = len(samples) # 標本平均 sample_mean = np.mean(samples) # 自由度N-1のt分布の上側2.5%点 t_a = stats.t.ppf(0.975, N - 1) # 信頼区間 x_0 = sample_mean - (t_a * (np.sqrt(S2 / N))) x_1 = sample_mean + (t_a * (np.sqrt(S2 / N))) print(x_0, x_1)
上のコードを実行してみると、この農園のみかんの平均重量は95%の確率で137.6gから158.6gの間に収まると評価することができます。この講座では正規分布を前提とした母平均の区間推定についてのみ解説しましたが、それら以外にも様々な分布や条件がありますので、分析したい標本に応じて使える分布を探してみてください。