データ集合が特定の分布に従うとき、そのデータの範囲を確率的に評価することが可能となります。このページでは比較的わかりやすい正規分布でパーセント点の求め方を解説します。
パーセント点
冒頭で書いたとおり、正規分布は範囲を確率的に評価することが可能です。例えば、農園Aのみかんの重量が以下の正規分布に従うことがわかっているとします。
- 平均:100g
- 標準偏差:5g
この場合、農園Aの適当なみかんはおおよそ95%の確率で92g以上、108g以下に収まると推定することができます。なぜそんなことがわかるのでしょうか?
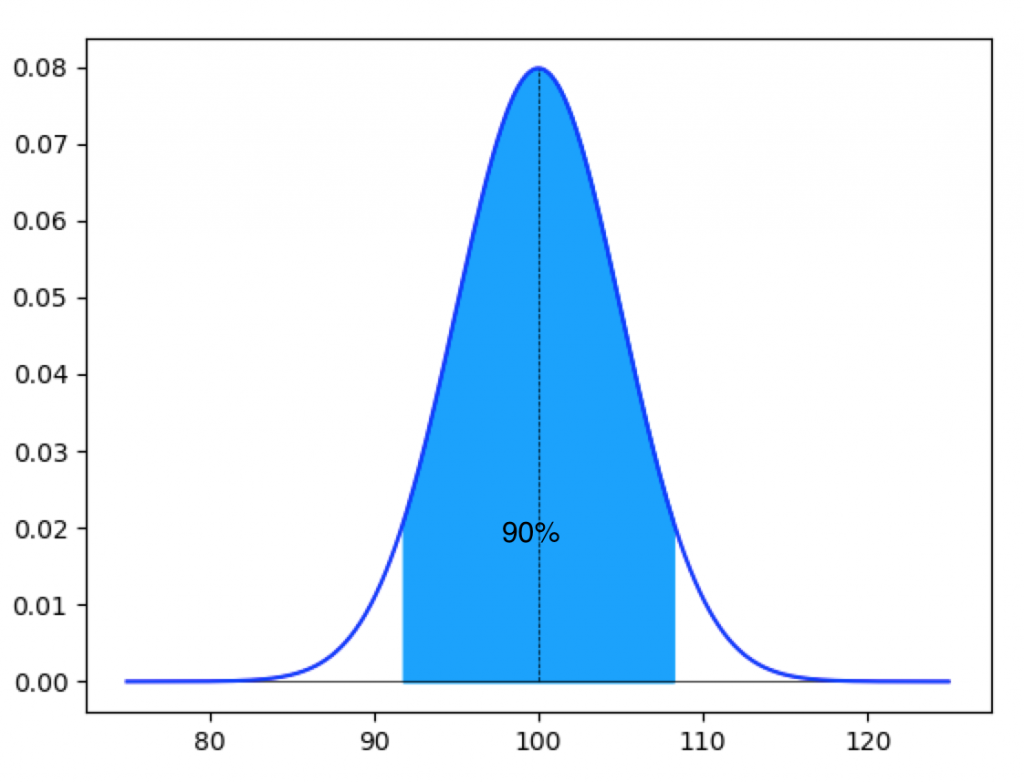
まず、この農園のデータ分布は以下のような正規分布のグラフで表すことができます。横軸は重量gを表します。平均値を釣り鐘の中心として左右対称となっています。以前説明しましたが、確率密度関数のグラフとX軸に囲まれた部分の面積は全体の確率1となります。
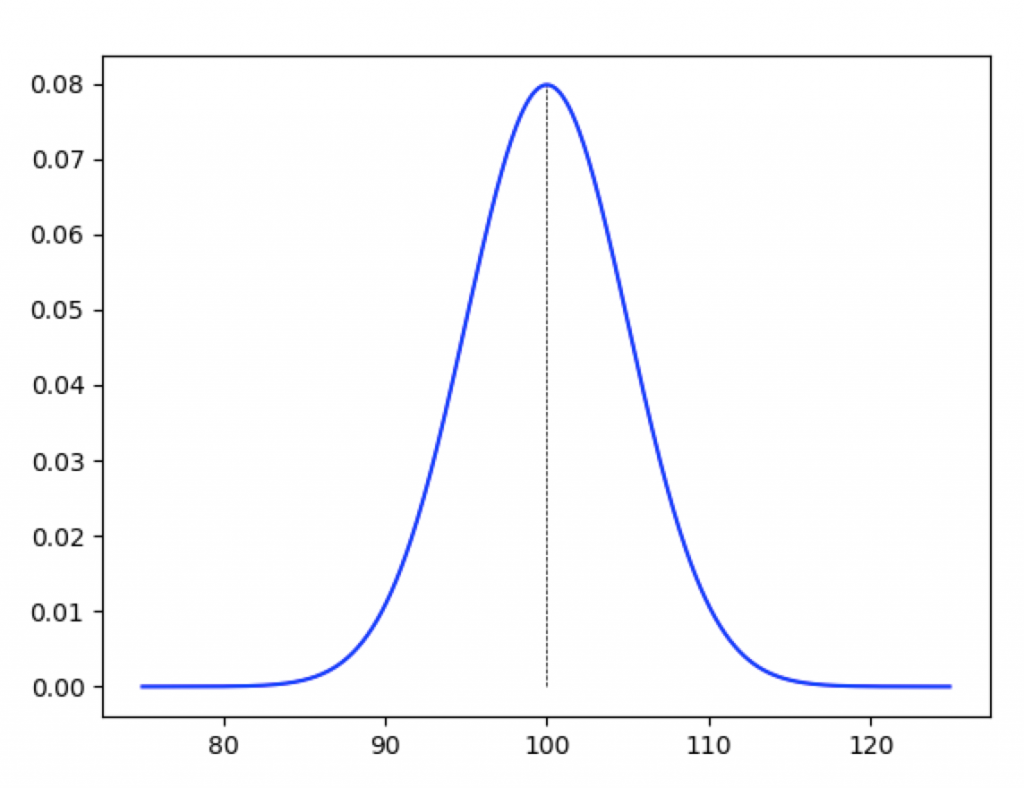
この関数は積分可能なので任意の範囲の面積、つまり任意の範囲の確率を求めることが可能です。例えば、このグラフの面積が0.05となる左側の境界を求めるとおおよそ92gとなります。(Pythonを利用した計算方法は後述します。)
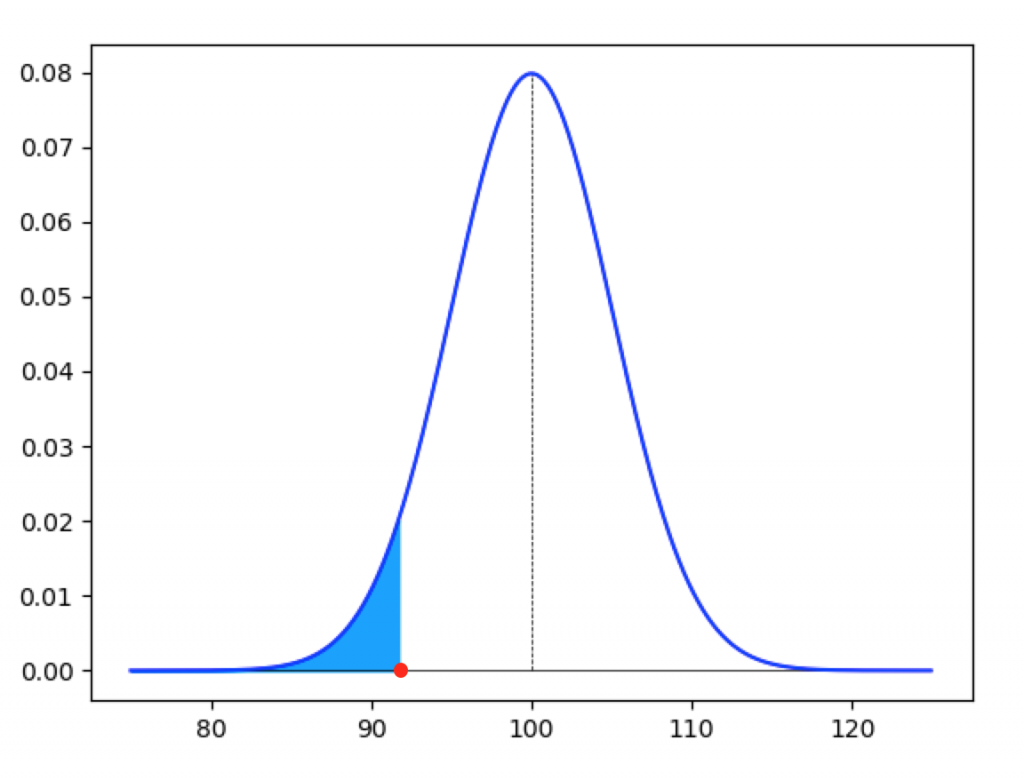
つまり、92g以下となる確率は5%となります。このような左側の確率を「下側5%点」と呼びます。
同様に右側の5%となる境界を求めると、108gとなります。つまり、108g以下となる確率は5%となります。このような左側の確率を「上側5%点」と呼びます。
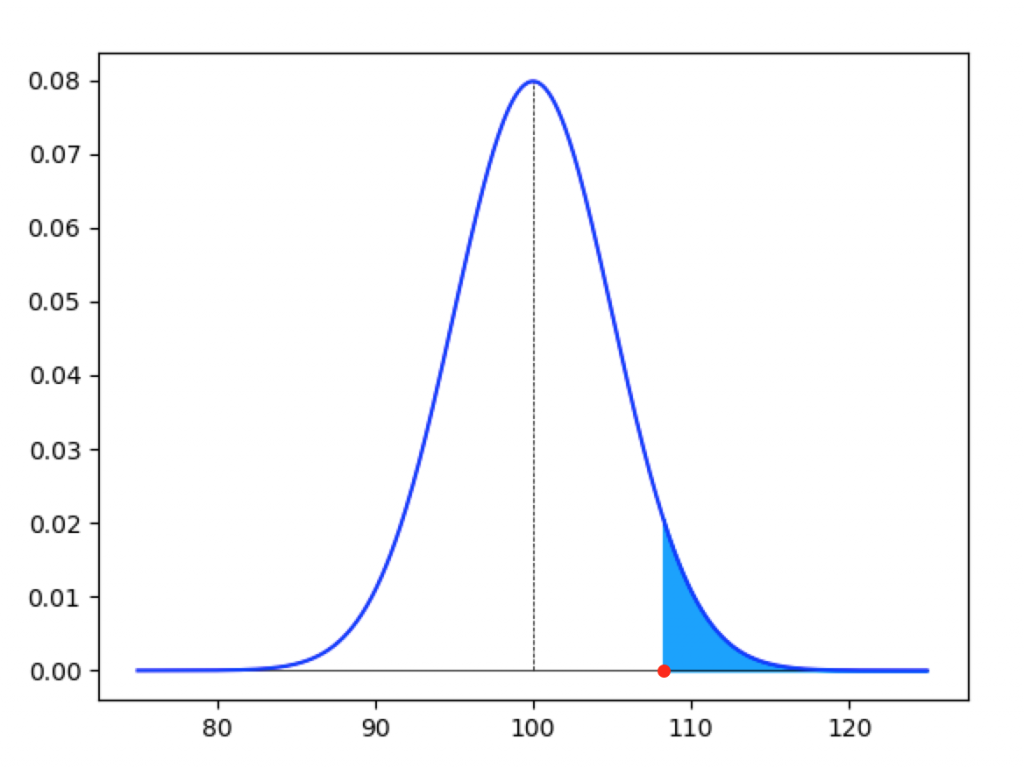
上側5%、下側5%で挟まれた部分は残りの90%となるため、先述の通り農園Aの適当なみかんはおおよそ95%の確率で92g以上、108g以下に収まると推定することができます。
パーセント点を求める
パーセント点を求める計算は積分を伴うため難しく、通常筆算で解く場合はは標準化を行い予め算出された標準正規分布表から導出することになるのですが、Pythonを使用すると簡単に値を求めることが可能です。前回グラフの描画に使用したscipy.statsのnormを使います。
例えば先程の例の平均:100、標準偏差:5の正規分布の左側5%点、右側5%点を求める場合、以下のようになります。
from scipy.stats import norm # mean loc = 100 # standard deviation scale = 5 p1 = norm.ppf(q=0.05, loc=loc, scale=scale) # 91.77... p2 = norm.ppf(q=0.95, loc=loc, scale=scale) # 108.22...
ある点が何%点かを求める
また逆に、正規分布を前提としてX軸のある点が何%点となるのか?を求める場合もあります。例をみてみましょう。
ある工場では製品に品質管理用の製品評価指数を設けており、この指数は以下の正規分布に従うことがわかっているとします。
- 平均:100
- 標準偏差:3
この製品評価指数が90を下回る製品は不良品扱いとして出荷しないことにしました。不良品が発生する確率は何%になるでしょうか?
前提条件より以下の正規分布グラフとなります。90より左側の面積を求めることになります。
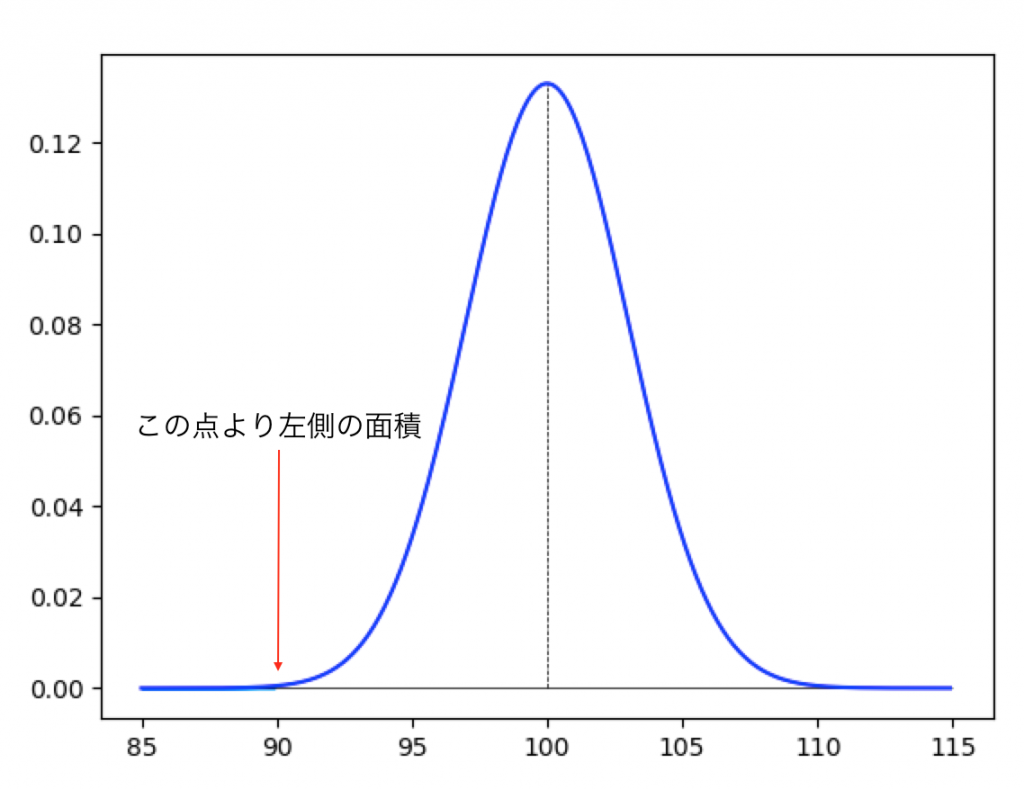
Pythonで求める場合、scipy.statsのcdfを利用します。
実際計算を実行してみると、以下のようになります。
from scipy.stats import norm # mean loc = 100 # standard deviation scale = 3 p = norm.cdf(x=90, loc=loc, scale=scale) # 0.00042
計算結果より、不良品扱いとなる製品の割合は1万個に4つ程度となることがわかりました。
まとめ
このパーセント点を求める操作が統計学の入門部分の一つの肝で、ここができれば今後説明する区間推定や帰無仮説検定の理解がスムーズかと思います。また、今回は正規分布を利用しましたが、正規分布以外でもパーセント点を求められる場合が多々ありますので様々に活用することができるようになるはずです。