前回、「データの中心」を表す統計量、平均、中央値、最頻値について解説しました。今回はデータの散らばりぐらい、「分散」と「標準偏差」について解説します。
分散
平均が同じでも・・・
前回の最後にデータの中心が同じでもデータの分布が異なることは多々あるという話をしました。もう一度グラフを確認してみましょう。
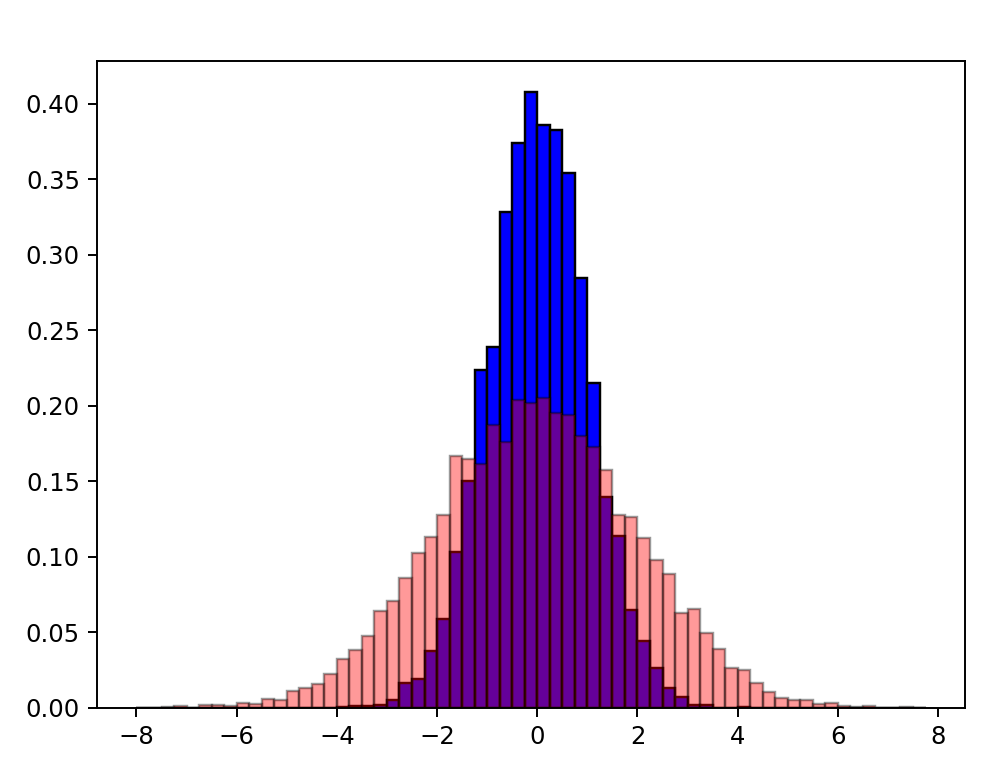
赤と青のグラフですが、データの散らばり具合が異なります。赤の方が、データの中心たる平均から遠くにまでデータが存在していてデータのばらつきが大きいといえます。
このばらつきを数学的に扱う方法を考えてみましょう。各値の平均からの距離の絶対値の合計でも良さそうなので、N個のデータのばらつきを表すために、まず考えられるのは以下の式ではないでしょうか。\(\overline{x}\)は平均を表します。
\[
\frac{|x_1 - \overline{x}| + |x_2 - \overline{x}| + \cdots + |x_N - \overline{x}|}{N}
\]
一言で書くと「平均からの絶対値距離の平均」となります。(絶対値を省くと平均からの距離の平均となり、常に0になるため使い物になりません。)以下に数式のイメージを載せます。
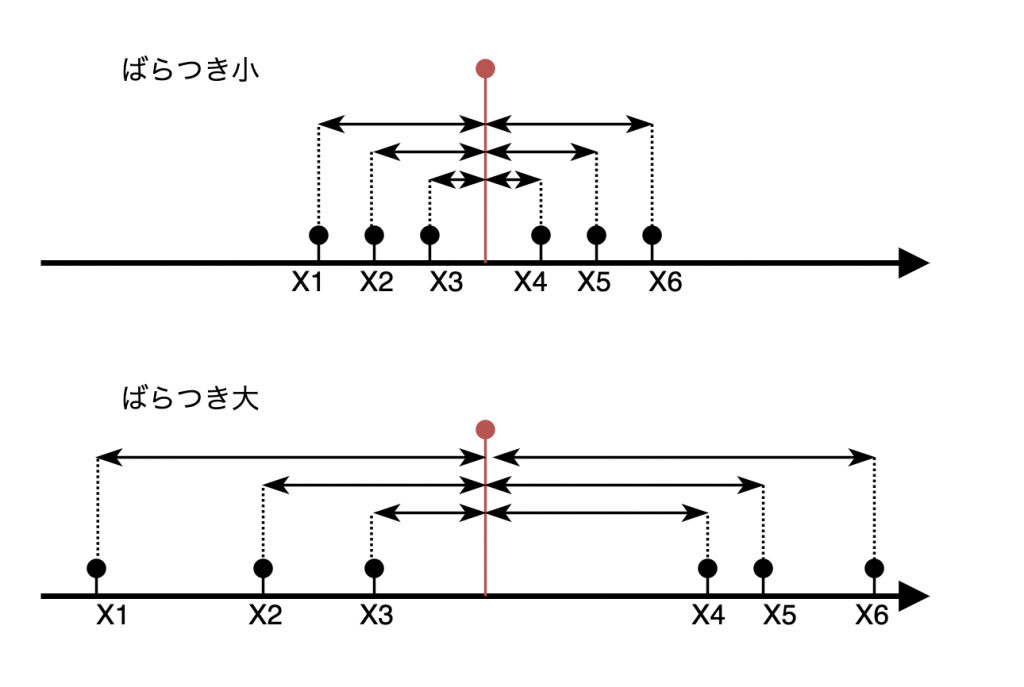
上の2つの図のは点x1〜x6が数直線上に配置されています。赤い目印がそれぞれの平均とします。矢印の長さの平均が先程の式の意味するところとなります。上段と下段とでは見た感じ下段のほうがばらつきが大きいですが、実際矢印の長さの合計は下段のほうが大きいため、ばらつきの大きさが評価できていることが感覚的にわかります。
この式は平均偏差と呼ばれるもので直感的にわかりやすくコンセプトとして重要なのですが、式の中に絶対値が入っているため微分ができないといった「数学的に扱いにくい」ため、あまり使われません。なお、偏差とは平均からの距離のこと指します。
分散
そこで平均偏差を数学的に扱いやすい形にしたのが分散です。以下の式で表されます。
\[
\sigma^2 = \frac{(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + \cdots + (x_N - \overline{x})^2}{N}
\]
\[
= \frac{1}{N} \sum_{k=1}^{N} (x_k - \overline{x})^2
\]
絶対値の代わりに2乗しているわけですね。計算式だけ見ると難しそうですが、成り立ちがわかっていると暗記する必要がないことがわかると思います。なお、分散の記号は\(\sigma^2\)(しぐまじじょう)と表します。
データ配列の分散をPythonで求めるには以下のようにnumpyのvarを使用します。
import numpy as np data = [2, 5, 3, 10, 7, 2, 10] np.var(data) # 10.530....
では練習です。2つのクラスA、Bがあり、それぞれのクラスの生徒の身長は以下の通りであったとします。A、Bともに平均は170cmなのですが、どちらのクラスの生徒のほうが身長のばらつきが大きいと言えるでしょうか?身長の単位はcmとします。
A=[165,168,171,177,171,162,163,166,168,187,172,177] B=[188,161,174,155,184,187,160,158,178,175,160,165]
さっそく分散を計算してみましょう。
import numpy as np import pandas as pd from matplotlib import pyplot as plt # クラスA、Bの生徒の身長 A=[165,168,171,177,171,162,163,166,168,187,172,177] B=[188,161,174,155,184,187,160,158,178,175,160,165] # 分散を算出 np.var(A) # 45.9... np.var(B) # 132.2...
分散を比較するとクラスBの生徒のほうが身長のばらつきが大きい、といえます。
標準偏差
分散の単位
分散でデータのばらつきが評価できるようになりましたが、単位の問題があります。2乗の和なので単位も2乗となります。例えば先程のデータ、分散の単位はcm^2なのですが意味を捉えづらくなっています。
標準偏差
これを解決するには分散に対して単純に√を被せればよく、以下の式を標準偏差と呼びます。
\[
\sigma = \sqrt{\sigma^2} = \sqrt{\frac{\sum_{k=1}^{N} (x_k - \overline{x})^2}{N}}
\]
標準偏差は\(\sigma\)で表します。
また、データ配列の標準偏差をPythonで求めるには以下のようにstdを使用します。
import numpy as np data = [2, 5, 3, 10, 7, 2, 10] np.std(data) # 3.245...
では練習としてさきほどの生徒の身長の標準偏差をPythonで計算してみましょう。
import numpy as np import pandas as pd from matplotlib import pyplot as plt # クラスA、Bの生徒の身長 A=[165,168,171,177,171,162,163,166,168,187,172,177] B=[188,161,174,155,184,187,160,158,178,175,160,165] # 標準偏差を算出 np.std(A) # 6.77... np.std(B) # 11.49...
これで先程のデータの標準偏差は6.77cmと11.49cmと単位付きでばらつきがあわらすことができました。
このページではばらつきを表す方法として分散と標準偏差について解説しました。また、平均が同じ場合ののばらつき具合について評価しました。次回は変動係数をつかって異なる単位や平均が大きく異なるデータセットでのばらつきの評価方法について解説します。




