前回はデータをヒストグラムで表し、特徴を観察しました。今回はデータの中心を表す統計量を算出してみましょう。
統計量とデータの中心
統計量とはデータを要約する値のことです。統計分析の目的の1つは、データの特徴を結論付けをすることが挙げられます。データの特徴を表す統計量は様々なのですが、最初に学習すべき統計量としてデータの中心を表す平均、中央値、最頻値があります。
平均
まずは平均からです。統計分析ではミーンと呼ぶ場合が多いです。平均はすべてのデータの和を個数で割り算して算出します。値1〜値NのN個のデータが与えられていた場合、平均は以下の式となります。データと特徴を知る上で最もよく使用される指標といえます。
\[
平均 = \frac{値1 + 値2 + ・・・ + 値N}{N}
\]
numpyを使用して配列の平均を算出する場合は以下のようになります。
import numpy as np # データ配列 data = np.array([1, 3, 5, 5, 8]) # 平均の算出 np.mean(data) # 4.4
中央値
すべてのデータを並べたときに中央となる値を中央値(メディアン)と呼びます。たとえば、1,2,3,7,10と5個のデータが与えられていた場合、順に並べた真ん中の3が中央値となります。
numpyを使用して配列の中央値を算出する場合は以下のようになります。
data = np.array([1,2,3,7,10]) np.median(data) # 3.0
最頻値
データのうち、最も頻度が高いデータ、簡単に書くと登場回数が多いデータを最頻値(モード)と呼びます。たとえば、1,2,2,3,3,5,5,5,7,7,10というデータが与えられていた場合、登場回数が最も多い5(3回登場)が最頻値となります。
最頻値を算出する場合scipyのstatを使用します。平均や中央値と異なり最頻値は「登場回数が最も多い値」と「登場回数」の2つの値がセットとなるため、オブジェクト形式となっています。
import numpy as np from scipy import stats data = np.array([1,2,2,3,3,5,5,5,7,7,10]) m = stats.mode(data) m.mode[0] # 5 m.count[0] # 3
4行目のstats.modeで最頻値を算出したいデータ配列を指定するとModeResultというオブジェクトが返されます。5〜6行目で最頻値と登場回数をModeResultから取得しています。また、stats.modeは多次元配列に対応しているためインデックスを指定する必要があります。今回は1次元データなのでインデックスに0を指定しています。
分布とデータの中心
3種類のデータの中心を求めることができるようになりました。ここでいくつかの注意点をあげてみたいと思います。
平均が真ん中とは限らない?
データ1件あたりの量を考える場合には平均が使いやすいですが、データの中心としての特徴を必ずしも表しているとは限りません。
ちょっとした例で考えてみましょう。あるサービスの会員ユーザーの年収を集計ししてみたとします。10人の会員の年収がそれぞれ350, 355, 410, 420, 430, 435, 500, 550, 600, 1980だったとします。会員の平均年収は600万円を超えますが、これらのユーザーに対して年収600万円台の人向けの広告を打つことは適切でしょうか?
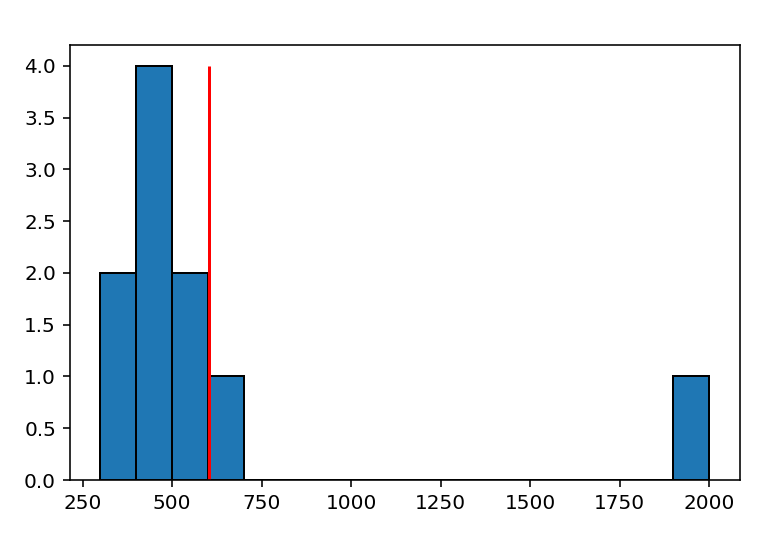
data = np.array([350, 355, 410, 420, 430, 435, 500, 550, 600, 1980]) np.mean(data) # 603.0 np.median(data) # 432.5 fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.hist(data, bins=range(300, 2100, 100),histtype='barstacked', ec='black') plt.show()
平均年収は600万円ですが、ヒストグラムで確認してみると中央値の430万円台を会員の年収の目安として考えたほうが良さそうです。実際、会員の9割が年収600万円以下となるため平均値を採用することは明らかに不適切です。
少し話がそれますが、業界や会社、年齢別と言った平均年収は、この例のように定まった下限と上側の外れ値のため、ほとんどの人が平均年収より下に属してしまう、といったことがよく起こるのでマーケティングのアプローチとして採用する場合は注意が必要です。
分布が左右対称でない、外れ値がある、下限があり上限がない、といったデータの場合は平均と中央値が異なることが一般的です。特に外れ値がある場合、中央値はその影響を受けにくいためデータの中心を考える際には適しています。中央値のような外れ値に対する安定性をロバスト性と呼びます。
ばらつき
平均や中央値といったデータの中心が同じだからと言ってもデータの分布が同じとは限りません。以下のデータ分布を見てください。
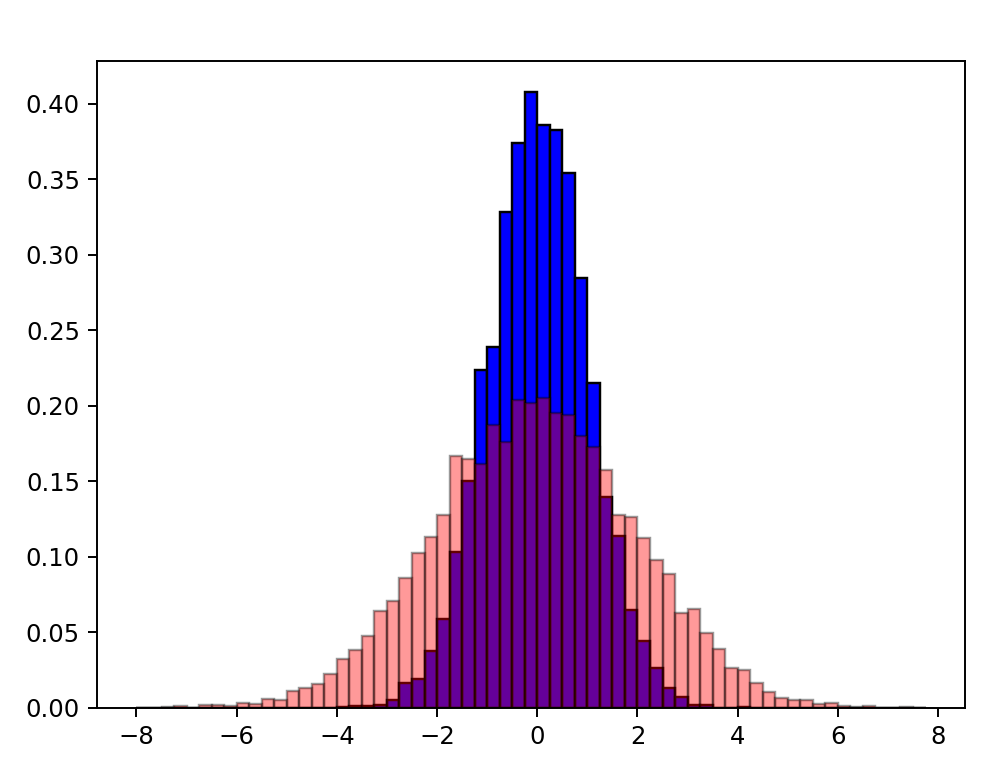
2つヒストグラムを重ねています。この2つデータの個数、平均、中央値が全く同じなのですが、裾野の広さやデータの高さといった分布の様子は明らかに異なります。これは、データのばらつきが異なることが原因です。次ページにてデータの中心と並んで重要なデータのばらつきに関する統計量について学習しましょう。