前回は記述統計と推計統計について解説しました。今回から推測統計を主に解説していきます。まずは点推定から学習しましょう。
平均の点推定
平均の点推定の式
点推定とは標本から母集団の統計量、平均や分散となる値そのものを推測する推測統計の手法の1つです。もっともこの点推定なのですが、平均を推測する際に日常的によく使っています。
例えばある国の人の平均身長を求めたいとき、「無作為にその国の人を何人かを選び身長を測り、その平均を求める」といった方法が思いつくのではないでしょうか。この方法こそまさに点推定そのもので、「ある程度標本サイズが大きければ母集団と標本とで平均は概ね同じだろう」といいうアイデアに基づいています。このため、平均の点推定は以下の式で与えられます。
平均 = \frac{値1 + 値2 + ・・・ + 値N}{N}
\]
普通の平均の式と同じですね。Numpyで計算する場合は以下のようになります。
import numpy as np x_bar = np.mean(標本データの配列)
例えば、ある農園のみかんの重量100件のCSVデータがあった場合、以下のようにして母集団の平均値を点推定することができます。
mikan-sample100.csv
import pandas as pd
import numpy as np
df = pd.read_csv('mikan-sample100.csv')
weight_array = np.array(df['weight'])
# 標本から母平均を点推定
np.mean(weight_array)
点推定に求められる性質
平均の点推定を求める式は上で紹介した式だけなのですが、統計量によっては点推定の式が何種類もある場合があります。このため、点推定においてどの式を使うべきなのかを考える上で使ういくつかの指標があります。
一致性
さきほどの「ある程度標本サイズが大きければ母集団と標本とで平均は概ね同じだろう」というアイデアですが、標本サイズを大きくすると母集団の統計量に収束する性質がある場合、一致性がある、と呼びます。非常に当たり前の話なのですが重要な性質です。
上の平均に一致性があることをPythonコードで確認してみます。母集団1000件のみかんの重量データがあったとします。その中から標本サイズを増やすと平均がどう変化するでしょうか。
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
df = pd.read_csv('mikan-all.csv')
weight_array = np.array(df['weight'])
# 母集団の平均値
mu = np.mean(weight_array)
print(mu)
# 標本の数を増やしながら平均を算出
start = 10
end = 1001
X = np.arange(start, end, 5)
Y = []
for n in range(start, end, 5):
sample = np.random.choice(weight_array, n, replace=False) # 標本をn件ランダム抽出
x_bar = np.mean(sample)
Y.append(x_bar)
# 母平均をプロット
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.hlines(mu, start, end, "black", linestyles='dashed')
# 標本平均をプロット
ax.plot(X, Y, color='blue')
plt.show()
標本は毎回ランダムに抽出しているため毎回結果が異なりますが、概ね以下のようなグラフが描画されるはずです。横軸は標本サイズとなります。
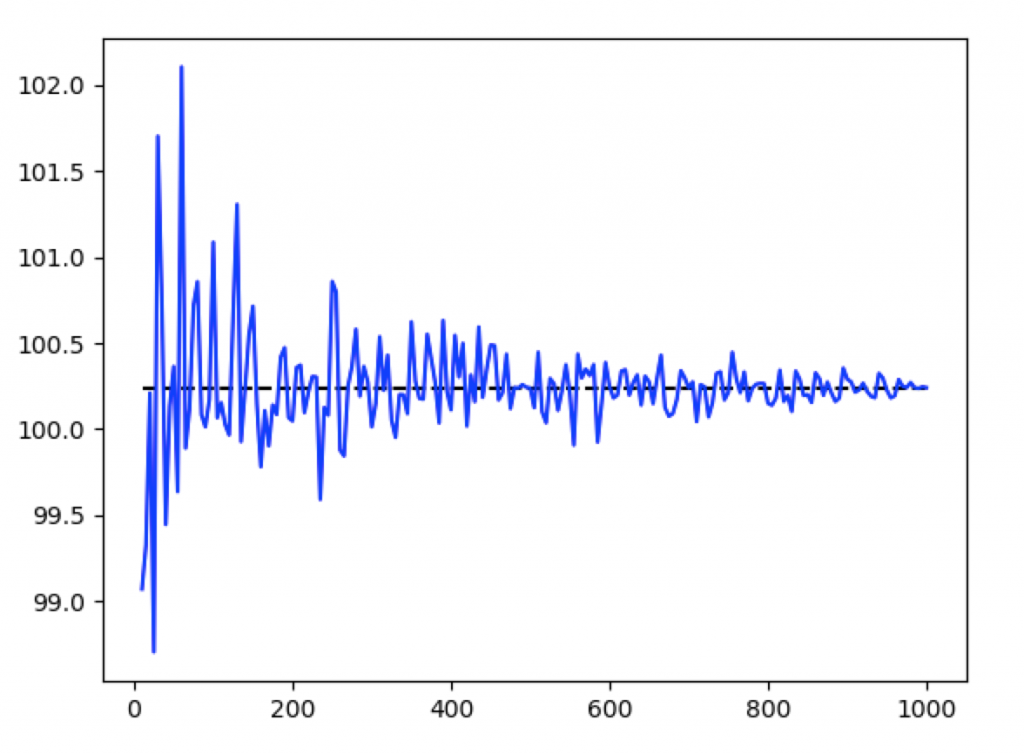
標本サイズが小さい場合はかなりの誤差が発生しています。また、標本サイズを大きくするにつれ推定値が収束していることが観察できます。ある程度標本サイズがないと信頼できないということが把握できると思います。
不偏性
また、「標本を選んで平均を取る」という操作は標本の選び方で毎回かわります。無作為抽出での標本平均は以下のようにこれもまた確率的に変わります。
1回目の平均:99g
2回目の平均:105g
3回目の平均:103g
:
:
これらの期待値、つまり平均が母集団の統計量と一致することを不偏性と呼びます。上の平均に不偏性があることをさきほどのみかんの重量のcsvファイルとPythonコードで確認してみましょう。
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
df = pd.read_csv('mikan-all.csv')
weight_array = np.array(df['weight'])
# 母集団の平均値
mu = np.mean(weight_array)
print(mu)
# 標本平均を500回計算
start = 0
end = 2000
X = np.arange(start, end, 1)
X_BAR = []
Y = []
for n in range(start, end):
samples = np.random.choice(weight_array, 200, replace=False) # 標本を200件ランダム抽出
x_bar = np.mean(samples) # 平均を算出
X_BAR.append(x_bar)
Y.append(np.mean(X_BAR)) # 平均の平均を算出
# 母平均をプロット
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.hlines(mu, start, end, "black", linestyles='dashed')
# 標本平均の平均をプロット
ax.plot(X, Y, color='blue')
plt.show()
標本平均を500回計算した平均が母集団の平均とある程度一致することが確認できます。
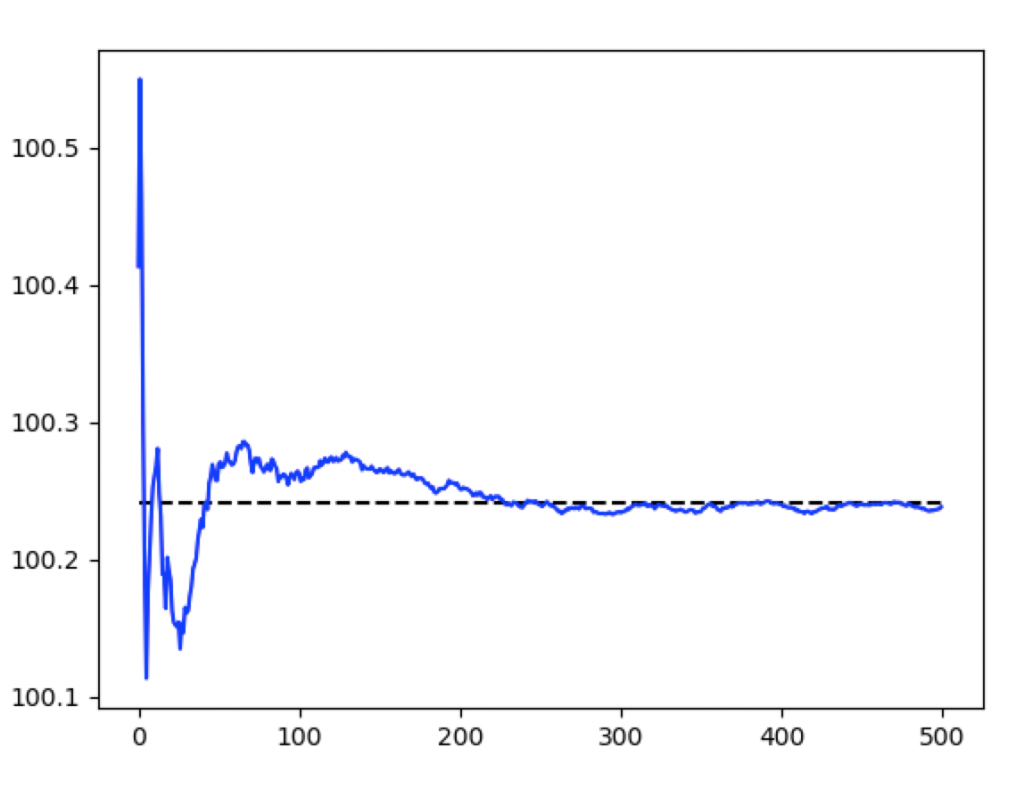
また、本講座では解説を割愛しますが一致性、不偏性以外に有効性、十分性や、最尤推定量といった考え方があります。
分散の点推定
分散の点推定では以下の式がよく使われます。標本分散と異なりn-1で割ります。この1は自由度と呼ばれています。
S^2 = \frac{1}{n-1}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2
\]
Pythonでnumpyを用いて求める場合、以下のようvarを使用します。ddofは自由度1を表しています。
import numpy as np np.var(データ配列, ddof=1)
さきほどの100個のみかんの標本から母集団の点推定をしてみましょう。
import pandas as pd
import numpy as np
df = pd.read_csv('mikan-sample100.csv')
weight_array = np.array(df['weight'])
# 分散の点推定
s2 = np.var(weight_array, ddof=1)
細かい確認は平均の時と同様なので割愛しますが、この分散の推定値は一致性と不偏性があります。標本分散と異なり不偏性があるため、不偏分散と呼ばれることもあります。