それではこのページからいよいよ統計分析手法について解説します。まず、データがどういった特徴を持っているのか、分布の有り様を調べるために、度数分布表とヒストグラムについて学習しましょう。
度数分布
度数分布表とは、データの区間ごとの数を集計した表です。1つの区間を階級と呼びますが、binと呼ぶこともあります。前回使用したirisデータを使用します。
前回の記事を読んでいない方は以下からcsvファイルをダウンロードしてください。
https://raw.githubusercontent.com/pandas-dev/pandas/master/pandas/tests/io/data/csv/iris.csv
import pandas as pd
import numpy as np
# データの読み込み
df = pd.read_csv('iris.csv')
# SepalLength列をndarrayに変換
data = np.array(df['SepalLength'])
# ヒストグラム
hist, bin_edges = np.histogram(data, bins=10)
パラメータは後ほど説明しますが、numpyのhistogram関数でhistgram形式の配列を得ることができます。変数histに各階級の数、bin_edgesに各階級の端点が格納されます。端点の数の方が多いため、bin_edgesの方が配列の要素数が多いという点に注意してください。
このままでは見づらいのでDataFrame形式に変換してみましょう。Spyderを使っている場合は変数エクスプローラでDataFrameの内容をきれいに表示することが可能です。
# 表示用に整形する
hist_df = pd.DataFrame(columns=["start","end","count"])
for idx, val in enumerate(hist):
start = round(bin_edges[idx], 2)
end = round(bin_edges[idx + 1], 2)
hist_df.loc[idx] = [start, end, val]
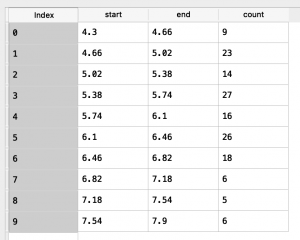
hist_dfの内容を確認してみましょう。10個の階級に分けた際、真ん中のほうが度数が大きいことがわかります。
ヒストグラム
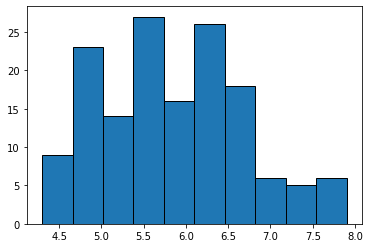
先程の度数分布表は階級ごとにデータがまとまっているものの、一見してデータの特徴を見出すことはなかなか難しいです。そこで登場するのがヒストグラムです。ヒストグラムは度数分布を棒グラフにして可視化したものです。matplotlibのhist関数でヒストグラムを描画することができます。引数のbinsで階級数を指定しています。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# データの読み込み
df = pd.read_csv('iris.csv')
# SepalLength列をndarrayに変換
data = np.array(df['SepalLength'])
# ヒストグラム
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.hist(data, bins=10, histtype='barstacked', ec='black')
plt.show()
度数分布表と比較して一目でデータの特徴が把握することができますね。
numpy.histgramとbins
np.histogram関数のパラメータについて解説します。以下の形式で使用します。
- a:対象となるデータ配列
- bins:階級数(int) or 階級(list))
- density:Trueの場合、ヒストグラムの面積が1となるように調整
binsは少し変わった引数で、整数を指定するとその数の区間に分割しますが、配列を指定するとその配列の階級となります。また、後述のスタージェスの公式で自動的に階級分けすることもできます。
plt.histは内部的にnumpy.histgramを使用しているのでplt.histでbinsの値による挙動の違いを確認してみましょう。
まずは引数に配列4〜8を指定してみます。
fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.hist(data, bins=[4, 5, 6, 7, 8], histtype='barstacked', ec='black')
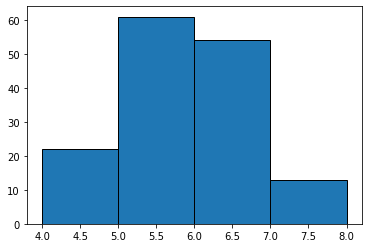
densityは、上の説明の通りヒストグラムの面積が1となるように調整してくれます。別ページで説明しますが、連続型の確率変数の場合は確率密度関数に近似させることが可能となります。
fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.hist(data, bins=[4, 5, 6, 7, 8], density=True, histtype='barstacked', ec='black')
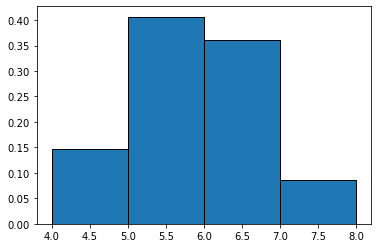
全体の面積が1なので、SepalLengthの値が5.0〜6.0となる割合(確率)は区間5〜6の面積0.4となります。このデータ元のアヤメの花のガクの長さはおおよそ40%の確率で5.0〜6.0に収まると推定することができます。
階級数の自動設定
階級の数は分析者が任意に定めることができるため、どのくらいの階級幅にするのか悩ましい場合があります。目安となる公式としてスタージェスの公式とフリードマン=ダイアコニスの法則の公式が挙げられます。スタージェスの公式とはデータの個数がnの場合、階級数は下式のkで与えられます。
\[
k=1+log_2 n
\]
フリードマン=ダイアコニスの法則の公式とは、データXの個数がnの場合、階級数は下式のkで与えられます。
\[
k=2 \times Xの四分位範囲 \times n^{(-1/3)}
\]
numpyのヒストグラムを利用する場合は自力で計算する必要はなく、bins='auto'を指定すると、スタージェスの公式とフリードマン=ダイアコニスの法則の公式の計算結果の内、両者ともに0より大きい場合は階級幅が小さいほうが自動で設定されます。先程のヒストグラムに対し、autoを使用してみましょう。
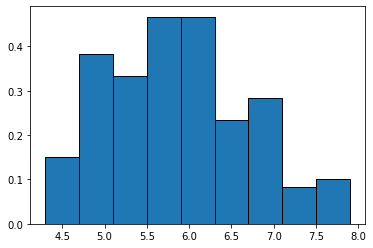
自動的に階級設定されていることがわかります。データを俯瞰する場合には使いやすいスタージェスの公式ですが、プレゼン等で人に見せる場合は人間がわかりやすい切りの良い数字で区切ったほうがよいかもしれません。
当初Rの仕様と混同しておりスタージェスが適用されると記述しておりましたが誤りです。上述の通りスタージェスが適用される場合とフリードマン=ダイアコニスがあります。あと、階級数ではなく階級幅でした。Numpyのhistgram.pyのソースコードのドキュメントも合わせてご参照ください。
Histogram bin estimator that uses the minimum width of the Freedman-Diaconis and Sturges estimators if the FD bandwidth is non zero and the Sturges estimator if the FD bandwidth is 0.