中心極限定理

標本次第で標本平均は様々な値をとるのですが、この平均値の分布について中心極限定理という非常に重要な性質があります。今回は中心極限定理について解説します。

中心極限定理とは

前回、平均と分散の点推定について解説しました。母集団の平均の点推定は標本の平均を使用します。当たり前なのですが、標本のとり方次第で平均値は確率的に様々な値となります。このため、標本平均は確率変数としてみなせるわけなのですが、この分布について非常に面白い性質があるのです。それが中心極限定理です。CLT(Central limit theorem)と略記されることがあります。

この定理のすごいところは母集団の分布に依らないという点です。（ただし厳密には母集団がコーシー分布といった平均が定義できないような特殊な分布では成立しません。）

「標本の平均値の分布」という点が少し分かりづらいかもしれません。少々雑ですが換言するならば「ある程度大きいサイズNの標本を何回か取り出して平均値\(\overline{X}_k\)（k回目の平均値）を求める試行を繰り返すと、1回目からn回目までの平均値\(\overline{X}_1\)〜\(\overline{X}_n\)の分布は正規分布として近似できる」ということです。

中心極限定理を確認してみる

では試しに適当な分布の母集団のデータセットに対し、1000個の標本を取り出して平均を求める試行を2000回繰り返してみましょう。今回は母集団の分布として0〜100の一様分布を使用してみます。numpy.radomのrandom_sampleで一様分布の乱数を引数で指定した数生成することができます。

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

# 母集団として0〜100の一様分布の乱数を10000個生成
X = np.random.random_sample(size=10000) * 100  # [0,1)の乱数を10000個生成し100倍
mu = np.mean(X)  # 母平均
sigma = np.std(X)  # 簿標準偏差

# サイズ1000の標本の平均を算出する試行を2000回行う
N = 1000
n = 2000

# figure、ax生成
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)

sample_means = []  # 標本平均のリスト

for i in range(n):
    # 標本抽出
    sample = np.random.choice(X, N, replace=True)
    # 標本平均を算出
    sample_mean = np.mean(sample)
    sample_means.append(sample_mean)

# 標本平均のヒストグラムを描画
ax.hist(sample_means, bins='auto', density=True, histtype='barstacked', ec='black')

# 平均mu、標準偏差sigma/√Nの正規分布グラフを描画
x_bar = mu
s = sigma / np.sqrt(N)
start = int(x_bar - s * 3)
end = int(x_bar + s * 3)
x = np.arange(start, end, 0.1)  # x軸範囲
norm_point = stats.norm.pdf(x, loc=x_bar, scale=s)

ax.plot(x, norm_point, linestyle='dashed', color='black')
plt.show()

出力結果は以下のようになります。正規分布とほぼ一致することが確認できます。

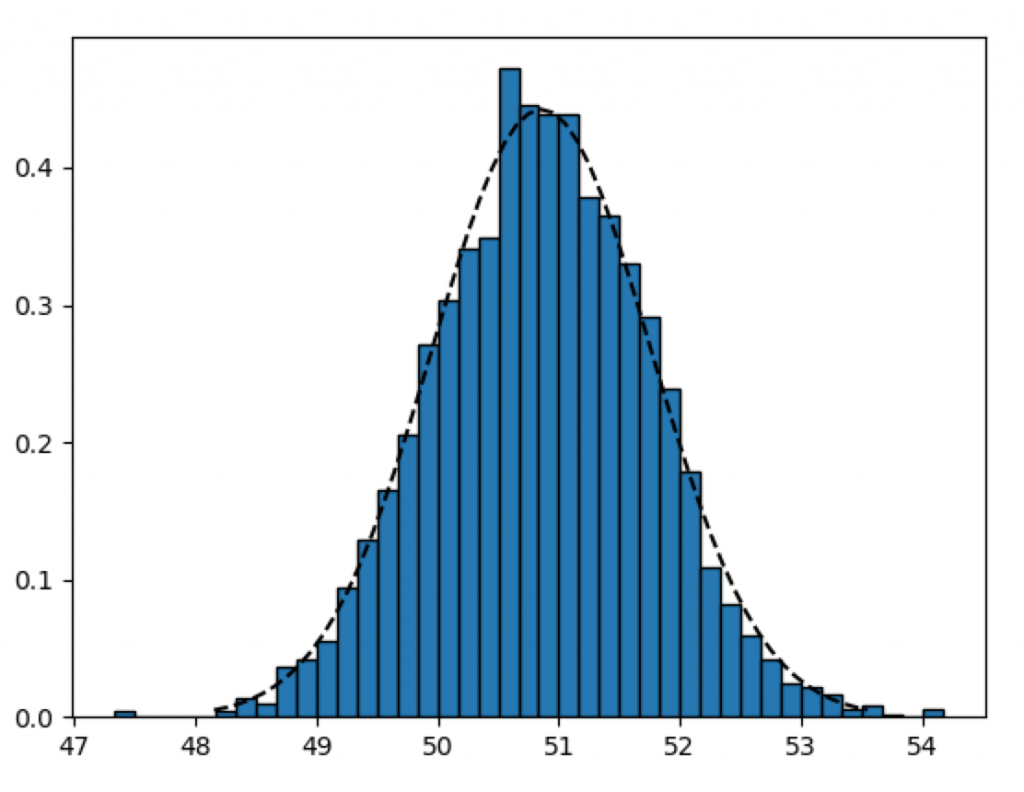
母集団が正規分布の場合は数学的に様々な良い性質が利用できるのですが、母集団の分布が正規分布ではない場合にも中心極限定理を利用することにより部分的に正規分布の特徴を利用することが可能となります。